ADC需要考虑的交调失真因素
发布日期:2024-02-20
点击次数:307
简介
交调失真(IMD)是用于衡量放大器、增益模块、混频器和其他射频元件线性度的一项常用指标。二阶和三阶交调截点(IP2和IP3)是这些规格参数的品质因素,以其为基础可以计算不同信号幅度下的失真积。虽然射频工程师们非常熟悉这些规格参数,但当将其用于ADC时往往会产生一些困惑。本教程首先在ADC的框架下对交调失真进行定义,然后指出将IP2和IP3的定义应用于ADC时必须采取的一些预防措施。
双音交调失真(IMD)
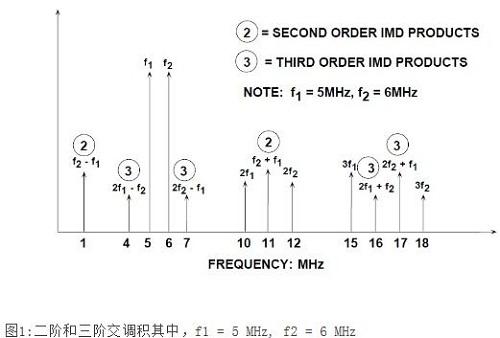
测量双音交调失真时,要将两个频谱纯净的正弦波在频率f1和f2下应用于ADC,这两个频率一般距离相对较近。将每个音的幅度设为比满量程低,数值略微超过6dB即可,以便两个音相位增加时,ADC不会出现削波。二阶和三阶积的位置如图1所示。请注意,二阶积处于数字滤波器可以消除的频率位置。然而,三阶积2f2-f1和2f1-f2接近原始信号,过滤的难度更大。除非另有说明,双音交调失真指这些"近距"三阶积。交调失真积值一般以dBc为单位,相对于两个原始音之一的值,而不是两者之和。
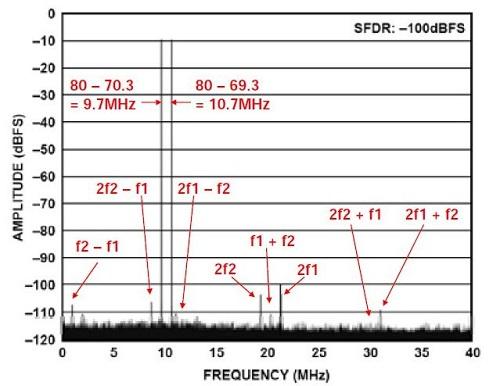 因此,混叠音出现在9.7MHz和10.7MHz,位于第一奈奎斯特区。图4同时显示了所有混叠IMD积的位置。高SFDR会增强接收器在有大信号时捕获小信号的能力,并防止小信号被大信号的交调积掩盖。图5所示为AD9444双音SFDR(为输入信号幅度的函数),其中,两个音的输入频率相同。
因此,混叠音出现在9.7MHz和10.7MHz,位于第一奈奎斯特区。图4同时显示了所有混叠IMD积的位置。高SFDR会增强接收器在有大信号时捕获小信号的能力,并防止小信号被大信号的交调积掩盖。图5所示为AD9444双音SFDR(为输入信号幅度的函数),其中,两个音的输入频率相同。

然而,请注意,如果两个音接近fs/4,则基波的混叠三次谐波可能使2f2-f1和2f1-f2真实积的识别变得异常困难。其原因在于,fs/4的三次谐波为3fs/4,而混叠出现在fs-3fs/4=fs/4频率处。类似地,如果两个音接近fs/3,则混叠二次谐波可能会干扰测量。原理同上,fs/3的二次谐波为2fs/3,混叠出现在fs-2fs/3=fs/3处。
二阶和三阶交调截点(IP2,IP3)、1-dB压缩点
三阶交调失真积在多通道通信系统中尤其麻烦,这种应用中,通道隔离在整个频段保持不变。三阶交调失真积在有大信号的情况下可能掩盖住小信号。
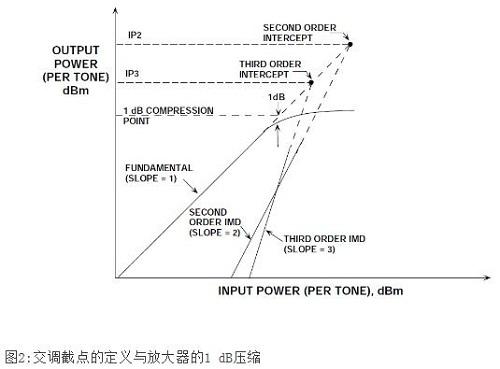
在放大器、混频器和其他射频元件中,一般以三阶交调截点(IP3)来表示三阶交调失真积,如图2所示。两个频谱纯洁的音被应用于该系统。单音的输出信号功率(单位:dBm)以及三阶积的相对幅度(以一个单音为基准)表示为输入信号功率的函数。基波表示为图中的slope=1曲线。如果通过幂级数展开逼近系统非线性度,则信号每增加1dB,二阶IMD(IMD2)幅度将增加2dB,如图中slope=2曲线所示。
类似地,信号每增加1dB,三阶IMD(IMD3)幅度就增加3dB,如图中slope=3曲线所示。
在一个低电平双音输入信号和两个数据点下,则可以绘制出二阶和三阶交调失真线,如图2所示(其原理是,一个点和一个斜率定义一条直线)。
然而,输入信号一旦达到某种水平,输出信号就会开始软限制或压缩。这里一个相关参数是1dB压缩点。这就是输出信号从一个理想的输入/输出传递函数压缩1dB的点。在图2中,该点处于理想斜率=1线变成虚线与实际响应表现出压缩迹象(实线)之间的区域中。
然而,二阶和三阶交调截线都可以延长,与理想输出信号线的延长线(虚线)相交。这些交点分别称为二阶和三阶交调截点,表示为IP2和IP3.这些功率电平值通常以传导至一个匹配负载(通常但不一定为50)的器件输出功率为基准,表示为dBm.
应当注意,IP2、IP3和1dB压缩点都是频率的函数,不出所料,频率越高,失真越严重。
对于给定的频率,在已知三阶交调截点的情况下,可以计算出三阶IMD积的近似电平值(为输出信号电平的函数)。

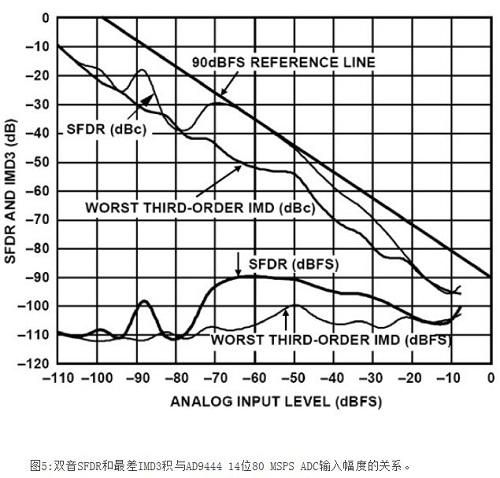
二阶和三阶交调截点的概念对ADC无效,因为,在这种情况下,失真积的变化不可预测(作为信号幅度的函数)。ADC并不是逐渐开始压缩接近满量程的信号(不存在1dB压缩点);一旦信号超过ADC输入范围,ADC就会充当硬限幅器,从而因削波而突然产生数量极大的失真。另一方面,对于远远低于满量程的信号,失真底保持相对稳定,不受信号电平影响,如图3所示。
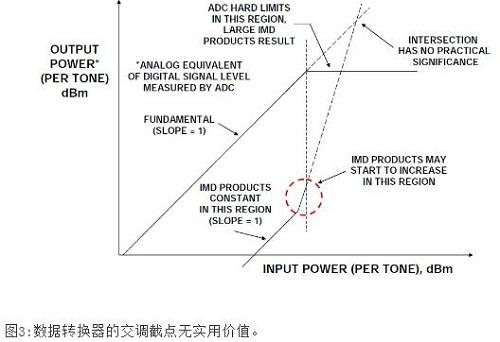

图3中的IMD曲线分为三个区域。对于低电平输入信号,IMD积保持相对稳定,不受信号电平的影响。这就意味着,当输入信号增加1dB时,该信号与IMD电平的比值也会增加1dB.
当输入信号处于ADC满量程范围的几dB之内时,IMD可能开始增加(但在设计优良的ADC中可能不会如此)。出现这种现象的确切电平取决于具体的ADC--有些ADC在其满量程输入范围内,其IMD积不会显着增大,但多数ADC会。当输入信号继续增加并超过满量程范围时,ADC应充当理想的限幅器,IMD积将变得非常大。出于对此类原因的考虑,ADC并无二阶和三阶IMD交调截点额定值。需要注意的是,DAC实际上存在同样的情况。在两种情况下,单音或多音SFDR(无杂散动态范围)额定值是广受认可的数据转换器失真性能的衡量指标。
多音无杂散动态范围
通信应用通常需要测量双音和多音SFDR.信号音数量越多,越接近蜂窝电话系统(如AMPS或GSM)的宽带频谱。图4所示为AD944414位80-MSPSADC的双音交调性能。两个输入音的频率分别为69.3MHz和70.3MHz,位于第二奈奎斯特区。


总结
交调失真(IMD2、IMD3)和交调截点(IP2、IP3)是混频器、LNA、增益模块、放大器等射频元件的常用规格参数。通过幂级数展开来模拟这些器件的非线性度,可以基于交调截点IP2和IP3来预测各种信号幅度的失真电平。与放大器和混频器不同,ADC失真(尤其是低电平信号)并不适用简单的幂级数展开模型,因此,交调截点IP2和IP3无法用于预测失真性能。另外,当输入信号超过满量程范围时,ADC将充当理想的限幅器,而放大器和混频器一般充当软限幅器。
尽管存在这些差异,但在通信应用中,了解ADC的双音IMD性能至关重要。较好的数据手册会针对多种输入信号频率和幅度提供这种数据。除此以外,ADIsimADCTM程序可用于评估各种ADC在系统应用要求的具体频率和幅度下的性能。ADIsimADC程序充当虚拟评估板的作用,可以从ADI网站下载,同时还可下载针对IF采样ADC的最新模型。该程序基于FFT引擎,可以精确地计算出单音和双音输入信号的SNR、SFDR和IMD值。
|
免责声明: 本文章转自其它平台,并不代表本站观点及立场。若有侵权或异议,请联系我们删除。谢谢! |










